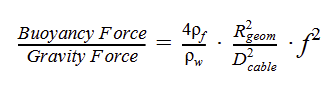Neutrally Buoyant Flexible Cables
In some subsea situations, you may want to have neutrally buoyant cables. A neutrally buoyant cable is one whose density is equal to the fluid around it (e.g., water) so that it remains in a specific position.
To create a neutrally buoyant flexible cable for a cable composed of a single wire:
- In the cable's Dynamics Properties extension:
- Set the Number of Wires field to 1.
- Make sure that the Density Unit field is set to Volumetric Density.
- Set the Density field of the single wire cable to match the known density of the desired fluid. For the cable to match the density of pure water, enter 1000 kg/m3.
- In the cable's Dynamics Generic Cable window:
- Under Parameters > Segment Definitions, make sure Fluid Definition is checked for all flexible segments.
- Also under Segment Definitions, set Collision Geometry Type to Capsule for all flexible segments.
- Under Parameters > Param Definition, set the Geometric Radius to half the Cable Diameter specified in the cable's Dynamics Properties extension.
Neutrally Buoyant Cables Composed of More Than One Wire
If the Number of Wires field in the Dynamics Properties is greater than 1, this means there is some void between the individual strands that make up the cable, reducing buoyancy. This wire void factor is given by the following table:
| Number of wires in cable | Wire Void Factor |
|---|---|
| 1 | 1.00000 |
| 2 | 0.50000 |
| 3 | 0.64617 |
| 4 | 0.68627 |
| 5 | 0.68522 |
| 6 | 0.66666 |
| 7 | 0.77778 |
| 8+ | 0.90700 |
The formula that gives the ratio between buoyancy and gravity is
where
- ρf is the density of the fluid
- ρw is the volumetric density of the cable
- Dcable is the cable diameter
- Rgeom is the cable's geometric radius
- f is the wire void factor
To have a neutrally buoyant cable, Buoyancy Force must equal Gravity Force, so the left hand side of the equation becomes 1. Given that the fluid density and void factor are set according to your scenario, you must the remaining variables to ensure that the right hand side equals the left hand side, i.e., 1.